Homework 7

Due Date:  Friday, October 24

1. In the following animation, the black point has coordinates \((0,0,\sin t)\) at time \(t\). The red line initially lies along the \(x\)-axis, and rotates at a rate of \(1\;\mathrm{rad}/\mathrm{sec}\) in the horizontal direction while also moving vertically.
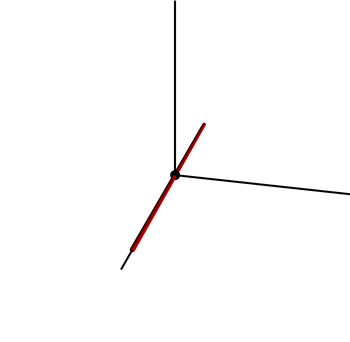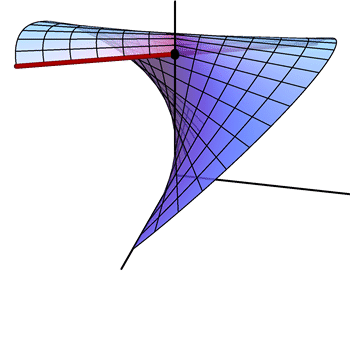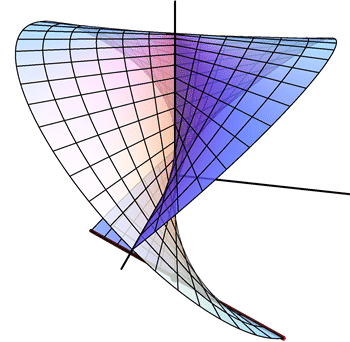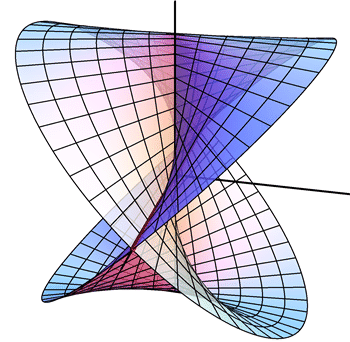
   1. Find parametric equations for the surface traced out by the red line.
   2. Find a Cartesian equation for this surface. Your answer should be a polynomial equation involving \(x\), \(y\), and \(z\).
2. The unit circle in the \(xy\)-plane begins rotating around the \(y\)-axis at a rate of \(1\;\mathrm{rad}/\mathrm{sec}\), while simultaneously moving in the \(y\) direction at a rate of \(1\;\mathrm{unit}/\mathrm{sec}\), as shown in the following animation Find parametric equations for the surface traced out by the circle.
3. Let \(T\) be the trefoil knot parameterized by \(\vec{x}(t) = \bigl(2 \sin 2t - \sin t,\) \(2\cos 2t + \cos t,\) \(\sin 3t\bigr)\). Find parametric equations for a surface whose boundary is \(T\), as shown in the following picture 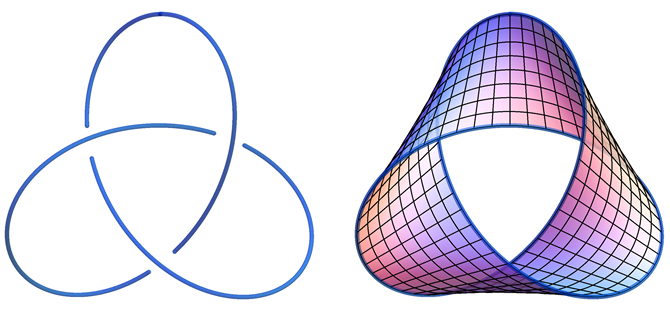Make sure to include bounds on \(u\) and \(v\) in your parameterization.