Jim Belk University of Glasgow

Homework 10

Due Date: Friday, December 4

Consider the fractal subset of \([0,1] \times [0,1]\) defined by the following iterated function system:

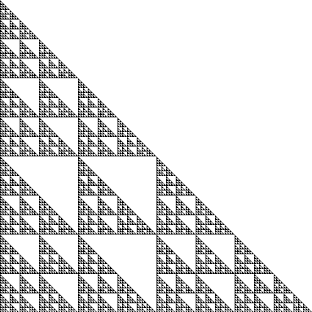\(\begin{align*} F_1(x,y) \;&=\; \left(\frac12 x,\,\frac12 y\right) \\[6pt] F_2(x,y) \;&=\; \left(\frac12 x + \frac12,\, \frac12 y\right) \\[6pt] F_3(x,y) \;&=\; \left(\frac12 x,\, \frac12 y + \frac12 \right) \\[6pt] F_4(x,y) \;&=\; \left(\frac14 x + \frac14,\, \frac14 y + \frac14\right) \end{align*} \)

Our goal is to determine the box-counting dimension of this fractal.

  1. Let \(B(n)\) denote the number of boxes in an \(n\times n\) grid that contain a point of this fractal. For example, \(B(2) = 3\) and \(B(4) = 10\). What is \(B(8)\)?
  2. Write a Mathematica notebook to determine the value of \(B(n)\) for \(n = \) \(16\), \(32\), \(64\), and \(128\). I suggest the following procedure:
    • First, compute at least 200,000 random points on the fractal.
    • Next, use the BinCounts command to tally the number of points in each box.
    • Finally, count the number of boxes containing at least one point from the fractal.
    Make sure to test that your code works for the data points mentioned in problem 1.
  3. The quantity \(B(n)\) should obey a power law of the form \[ B(n) \;\approx\; Cn^d, \] or equivalently \[ \log B(n) \;\approx\; (\log C) + d(\log n), \] where \(d\) is the box-counting dimension.
    1. Use the Mathematica to make a log-log plot of the data you have collected.
    2. Use the LinearModelFit command to fit the log-log data points to a linear function. Use only the four data points you found in problem 2.
    3. Make a plot showing the data points together with the linear regression line.
    4. What is the (approximate) box-counting dimension of this fractal?