Homework 1

Due Date:  Friday, September 5

1. An ellipse has foci at \((1,1)\) and \((-1,-1)\), and the point \((2,2)\) lies on its perimeter. Find an equation for this ellipse of the form \[ Ax^2 \,+\, Bxy \,+\, Cy^2 \;=\; D. \]
2. The following animation shows a unit circle rolling inside the circle \(x^2 + y^2 = 16\). 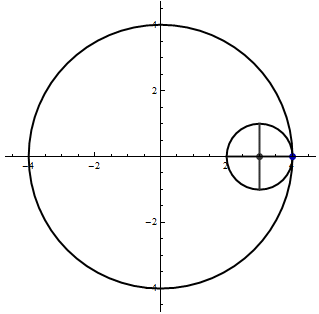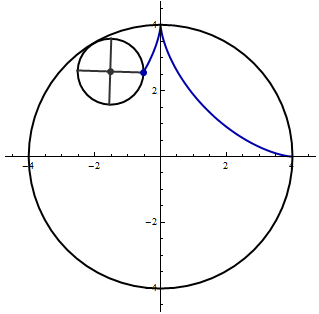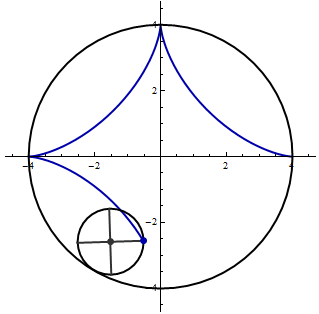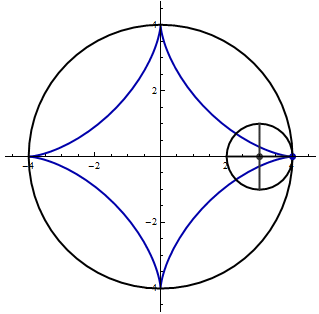Find parametric equations for the indicated curve.
3. The following animation shows a bar of length \(4\pi\) pivoting around the circle \(x^2 + y^2 = 1\). 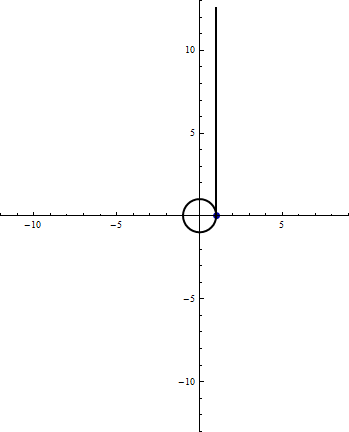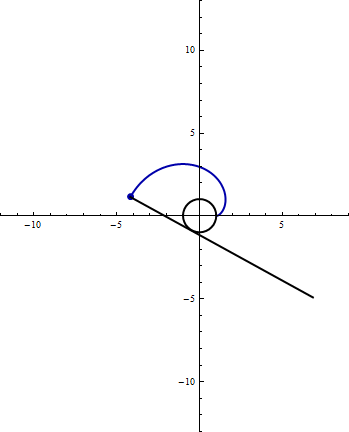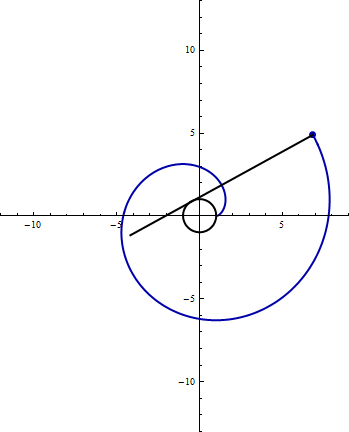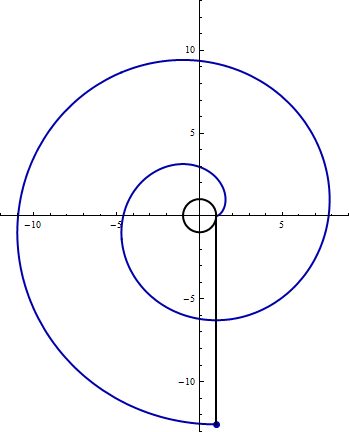Find parametric equations for the spiral traced out by the endpoint of the bar.
4. The following animation shows a perpendicular line segment of unit length moving along the inside of the parabola \(y=x^2\). 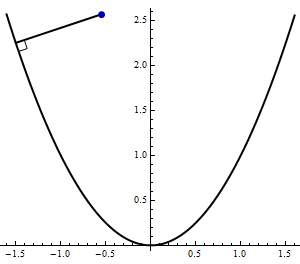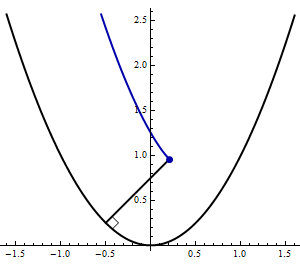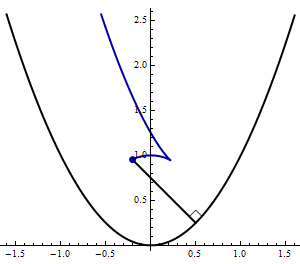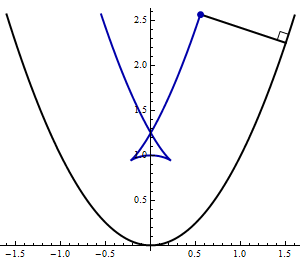Find parametric equations for the curve traced out by the other endpoint of the segment.