Homework 2
Due Date: Friday, September 12
- Evaluate \(\displaystyle\int_{\mathcal{C}} xy\,ds\), where \(\mathcal{C}\) is the portion of the ellipse \(4x^2 + 9y^2 = 36\) lying in the first quadrant.
-
- Let \(\mathcal{C}\) be any polar curve of the form \(r = f(\theta)\) for \(a\leq \theta \leq b\), where \(f\) is a differentiable function. Show that the arc length of \(\mathcal{C}\) is given by the integral \[ \int_a^b \!\sqrt{f(\theta)^2 + f'(\theta)^2}\,d\theta. \]
- Use the formula in part (a) to find the length of the curve \(r=e^{2\theta}\) between the points \((1,0)\) and \((0,e^\pi)\).
- The tractrix is the curve parametrized by \(\vec{x}(t) = (t-\mathrm{tanh}\,t,\mathrm{sech}\,t)\).
- Find the arc length function \(s(t)\) for the above parametrization.
- Find a unit speed parametrization of the tractrix. (Note: The \(y\)-component of your answer should not involve any hyperbolic trig functions.)
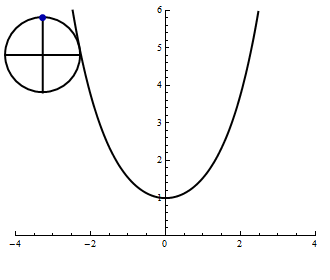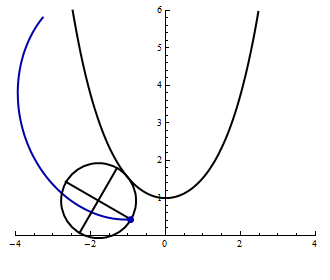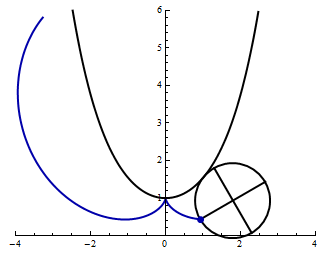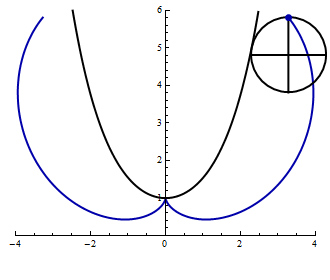
- The following animation shows a unit circle rolling along the bottom of the catenary \(y = \cosh x\). Find parametric equations for the indicated curve.