Homework 4

Due Date:  Friday, September 26

1. In the following animation, the black circle is the unit circle centered at the origin, and the red point is \((3,0)\). 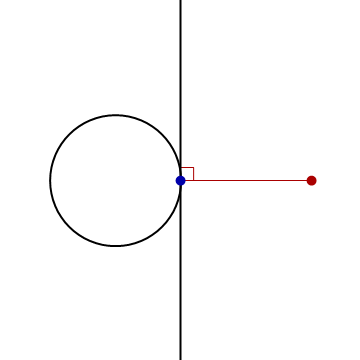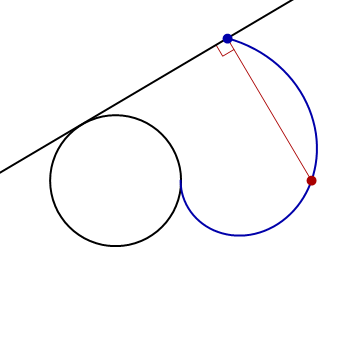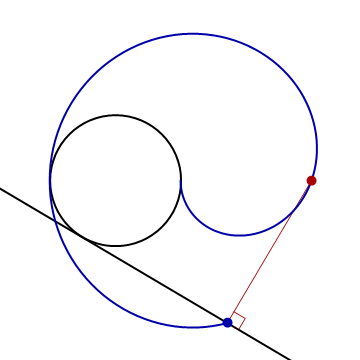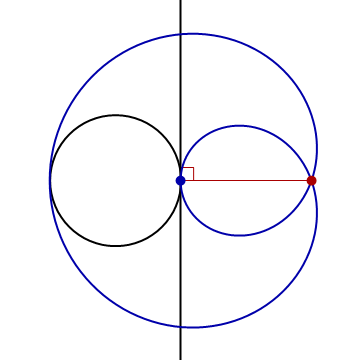Find parametric equations for the indicated curve.
2. Evaluate \(\displaystyle\int_{\mathcal{C}} \bigl(3x^2 + 6xy\bigr)dx + \bigl(3x^2 + 2y\bigr)dy\), where \(\mathcal{C}\) is the curve \(\vec{x}(t) = (2 \sin t,3\sin 5t)\) for \(0\leq t \leq \pi/2\).
3. For \(0\leq t \leq 1\), let \(L(t)\) be the line segment from the point \((0,1-t)\) to the point \((t,0)\).
   1. Find an equation for the line containing \(L(t)\). Your answer should have the form \(y = m(t)x + b(t)\), where \(m(t)\) and \(b(t)\) are functions of \(t\).
   2. Together, all of the line segments \(L(t)\) fill a region in the plane, as shown in the following animation. 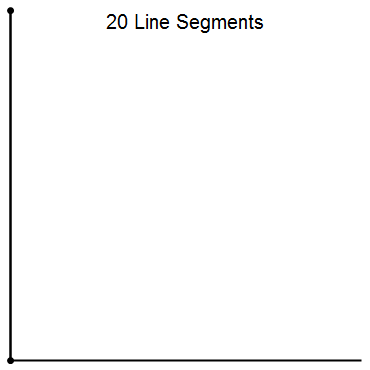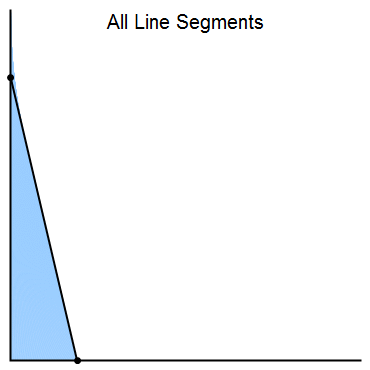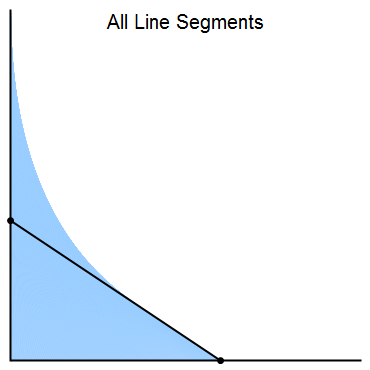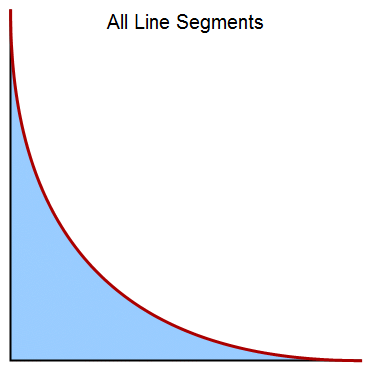Find parametric equations for the top boundary curve.
4. Find a differentiable function \(f(x)\) for \(-\pi/2 < x < \pi/2\) such that \(f(0) = f'(0) = 0\) and the curvature of the graph \(y = f(x)\) is \(\kappa_g(x) = \cos x\).

   Hint: Use the formula \[ \displaystyle\kappa_g(x) = \frac{f''(x)}{\bigl(1+f'(x)^2\bigr)^{3/2}} \] that we derived in class for the curvature of the graph of a function. Feel free to use a calculator or computer (e.g. Wolfram Alpha) to evaluate any integrals that arise.