Homework 5

Due Date:  Friday, October 10

Note:  When parameterizing curves, feel free to leave your answers in vector form, possibly including addition and scalar multiplication. For example, \[ \vec{x}(t) \;=\; \frac{1}{3}\left(1,1,1\right) \,+\, \frac{\cos t}{3}(2,-1,-1) \,+\, \frac{\sin t}{\sqrt{3}}(0,1,-1). \] is a perfectly good final answer.

1. The sphere \(x^2 + y^2 + z^2 = 25\) and the plane \(x + 2y + 2z = 9\) intersect along a circle \(C\). Find parametric equations for \(C\).
2. In the following animation, the black curve is the helix \(\vec{x}(t) = \bigl(\cos t,\sin t,\frac12 t\bigr)\), the black line is tangent to this helix, the red point is \((0,0,0)\), and the red and black lines are always perpendicular. 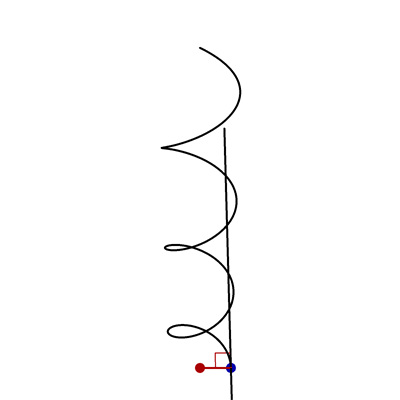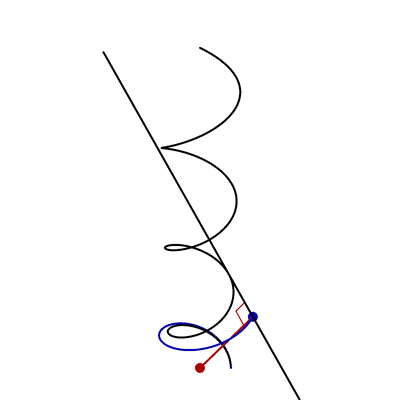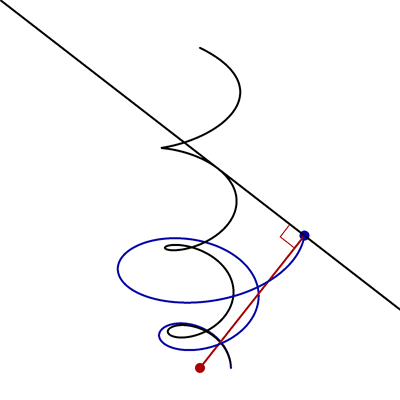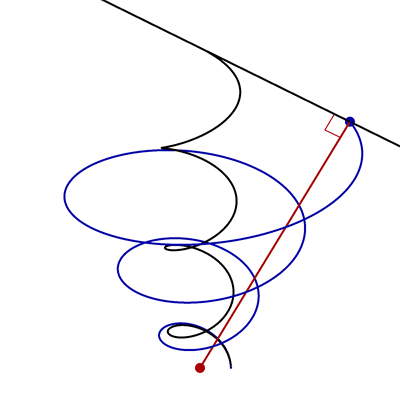Find parametric equations for the blue curve.
3. Let \(P\) be the parabola \(y=x^2\) in the \(xy\)-plane. Find parametric equations for the parabola that results from reflecting \(P\) across the plane \(x+y+z=1\).
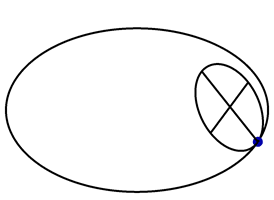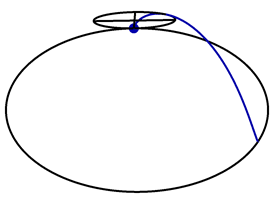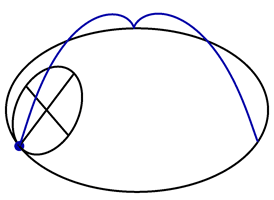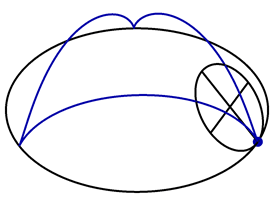
4. 1. A vertical circle with unit radius rolls along the circle \(\vec{x}(t) = (3\cos t,3\sin t,0)\), as shown in the following animation. 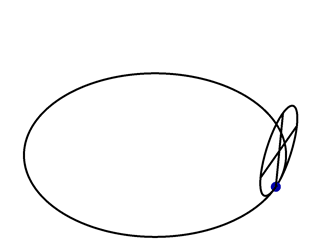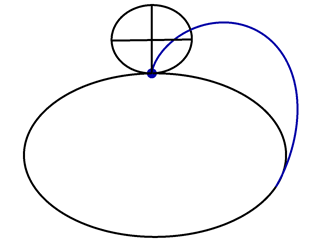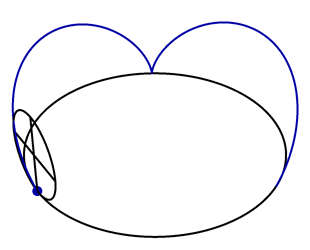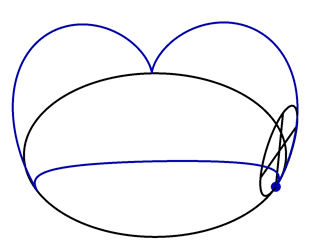A point \(\vec{P}(t)\) lies on the perimeter of the rolling circle, with \(\vec{P}(0) = (3,0,0)\). Find a formula for \(\vec{P}(t)\).
   2. Suppose instead that the rolling circle tilts inwards at a \(45^{\circ}\) angle, as shown in the following animation. Find a formula for \(\vec{P}(t)\) in this case.