Research
My research is a mix of group theory, dynamical systems, and topology.
Geometric Group Theory
My main research area is geometric group theory, which studies infinite discrete groups using tools from topology and geometry. Much of my work involves Thompson's groups and their generalizations, as well as automata groups, hyperbolic groups, mapping class groups, and so forth.
Within group theory, I am interested in embeddings between different groups as well as decision problems such as the word problem and conjugacy problem. Many of the groups I work with are infinite simple groups that have interesting cohomological finiteness properties. Such groups usually act by homeomorphisms on compact spaces, and I often use ideas from dynamical systems to study these homeomorphisms.
Complex Dynamics
I also do work in complex dynamics, which is the study of iterated holomorphic functions on the complex plane or Riemann sphere. I am particularly interested in Thurston's theorem, which characterizes the self-branched-covers of a sphere that are conjugate to rational maps. This is related to mapping class groups as well as the geometry of Teichmüller space.
I am also interested in the geometry and topology of the fractals that arise in complex dynamics, including Julia sets and the Mandelbrot set. Bradley Forrest and I have two papers on discrete groups of homeomorphisms of Julia sets, and more recently we have been investigating the quasiconformal geometry of polynomial Julia sets.
Publications
See the publications section of my CV for a concise list of my publications and preprints.
 |
A short proof of Rubin's theorem, with Luna Elliott and Francesco Matucci We give a short proof of a theorem due to Matatyahu Rubin, which states that a locally dense action of a group G on a locally compact Hausdorff space without isolated points is unique up to conjugation by G-equivariant homeomorphisms. This theorem is used in geometric group theory to show that isomorphisms between certain pairs of groups must be induced by homeomorphisms between spaces on which the groups act. Our proof uses ultrafilters on a certain poset to reconstruct the space from the group. |
 |
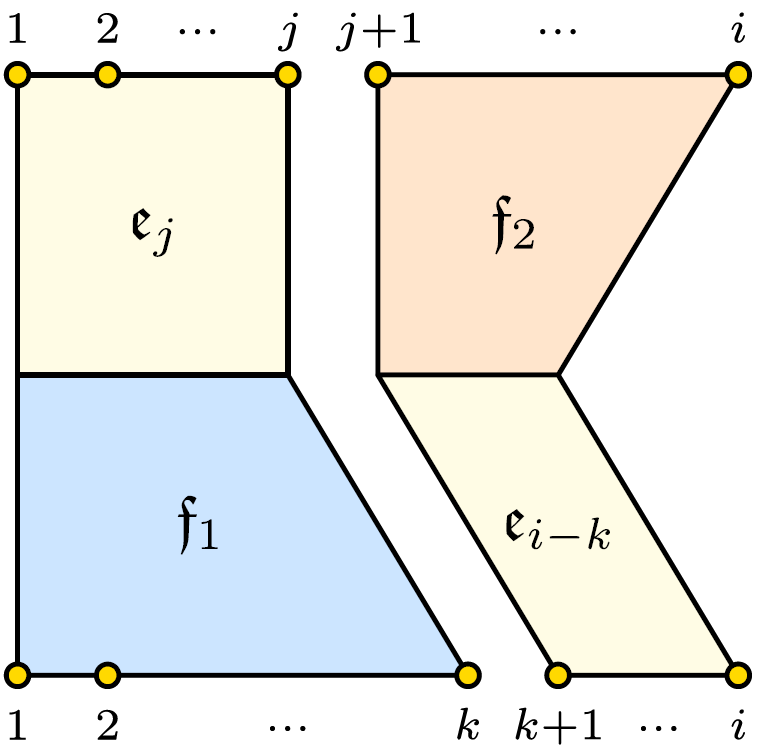Conjugator length in Thompson's groups, with Francesco Matucci We prove Thompson's group F has quadratic conjugator length function. That is, for any two conjugate elements of F of length n or less, there exists an element of F of quadratic length in n that conjugates one to the other. Moreover, there exist conjugate pairs of elements of F of length at most n such that the shortest conjugator between them has quadratric length in n. This latter statement holds for T and V as well. |
 |
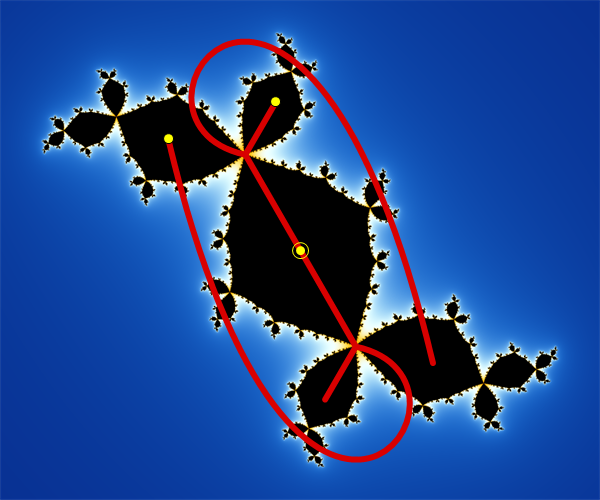Recognizing topological polynomials by lifting trees This is my main complex dynamics paper. We describe a tree-lifting algorithm that recognizes the Thurston class of a given topological polynomial. The algorithm produces either the Hubbard tree for a polynomial in the same Thurston class, or the canonical obstruction if the given topological polynomial is obstructed. Our proof solves Pilgrim's finite global attractors problem for polynomials, and we demonstrate our methods by solving some generalizations of Hubbard's twisted rabbit problem. Further applications of our methods have been given by Lanier and Winarski and by Mukundan and Winarski, and Jiang has examined the geometry of the complex of trees that we introduced. |
 |
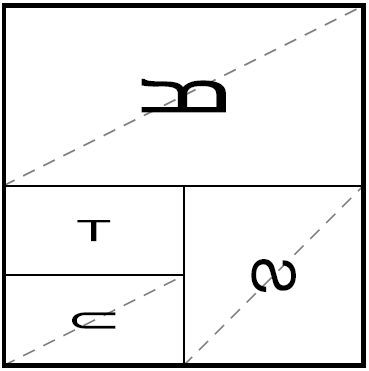
Embedding Q into a finitely presented group We give the first explicit, natural example of a finitely presented group that contains the additive group Q of the rational numbers. The finitely presented group in question consists of all “lifts” of elements of Thompson's group T to the real line. |
 |
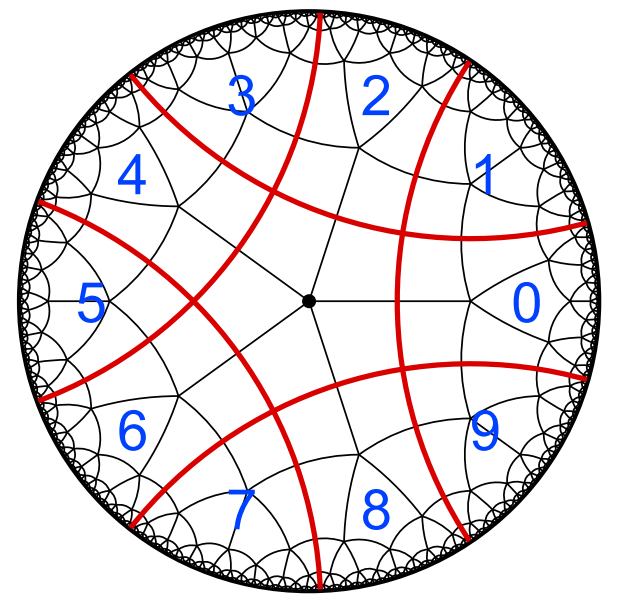
Twisted Brin–Thompson groups, with Matthew C.B. Zaremsky We define a new family of infinite simple groups that generalizes Brin's higher-dimensional Thompson groups, and we explore their finiteness properties. Using this construction, we prove that every finitely generated group embeds isometrically into a finitely generated simple group, and that every “Thompson-like” group embeds into a finitely presented simple group. We also exhibit a sequence of finitely presented simple groups that have arbitrary finiteness lengths. Matt Zaremsky has a follow-up paper that explores these ideas further. |
 |
Rational embeddings of hyperbolic groups We describe a symbolic coding of the horofunction boundary of a hyperbolic group, and show that the group acts on the codes via asynchronous Mealy automata. The codes arise from a self-similar structure on the tree of atoms for a hyperbolic group. It follows that every hyperbolic group embeds into the “rational group” of all asynchronous automata defined by Grigorchuk, Nekrashevych, and Sushchanskiĭ. |
 |
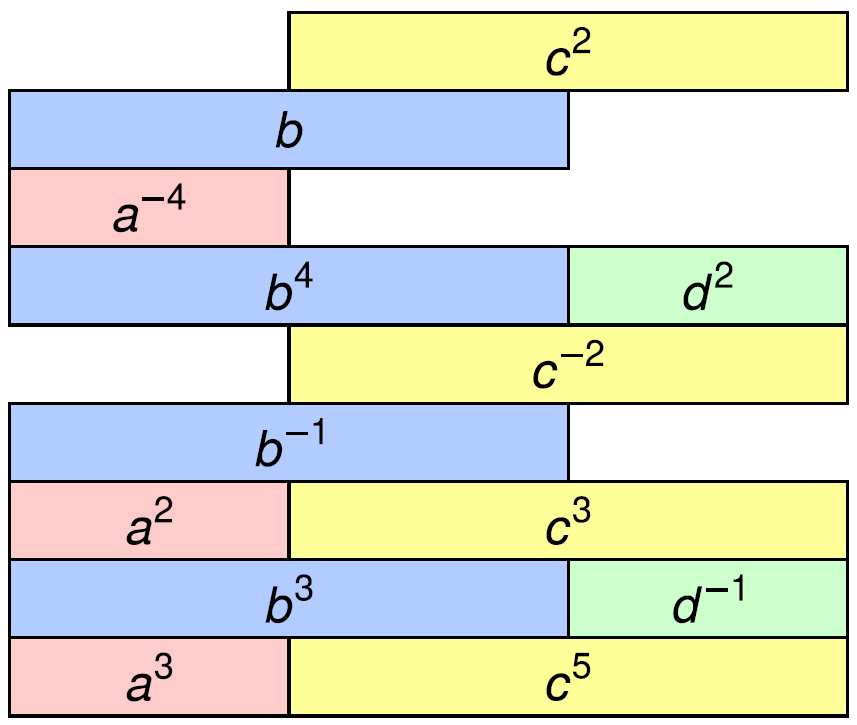Embedding right-angled Artin groups into Brin–Thompson groups We prove that every virtually special group embeds into a finitely presented simple group. Virtually special groups are a large class of groups defined by Haglund and Wise that include all right-angled Artin groups, all Coxeter groups, and many hyperbolic groups. To be specific, we show that all such groups embed into one of the higher-dimensional Thompson groups nV defined by Matthew Brin. Our bound on the dimension n was subsequently improved by Kato and then improved further by Salo. |
 |
On the asynchronous rational group,
with James Hyde and Francesco Matucci We prove that the “rational group” of all asynchronous Mealy automata defined by Grigorchuk, Nekrashevych, and Sushchanskiĭ is simple but not finitely generated. The rational group is interesting because it contains all self-similar groups as well as many Thompson-like groups, including the Lodha–Moore group and all Röver–Nekrashevych groups. |
 |
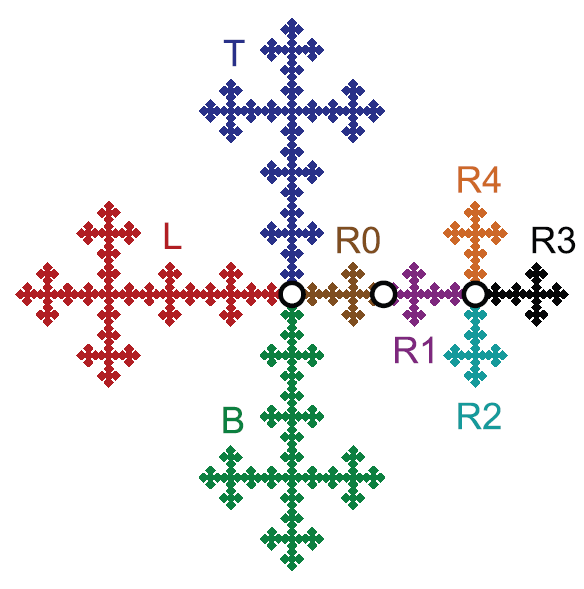Rearrangement groups of fractals, with Bradley Forrest We define a new family of Thompson-like groups acting on a variety of fractal spaces, including many Julia sets as well as some self-similar fractals such as the Vicsek fractal. We show that each of these groups acts on a naturally defined CAT(0) cubical complex, and that certain groups in this class have type F∞. Matteo Tarocchi has subsequently examined the structure of the rearrangement group for the airplane Julia set, and he and Davide Perego have proven that a class of rearrangement groups are not invariably generated. |
 |
Some undecidability results for asynchronous transducers and the Brin–Thompson group 2V, with Collin Bleak We show that every complete, reversible Turing machine is conjugate as a dynamical system to an element of Brin's group 2V. We deduce that 2V has unsolvable order problem, i.e. there is no algorithm to decide whether a given element has finite order. We also show that 2V can be represented as a group of asynchronous Mealy automata, and therefore the order problem for such automata is unsolvable as well. Ville Salo has subsequently proven that 2V also has unsolvable conjugacy problem. |
 |
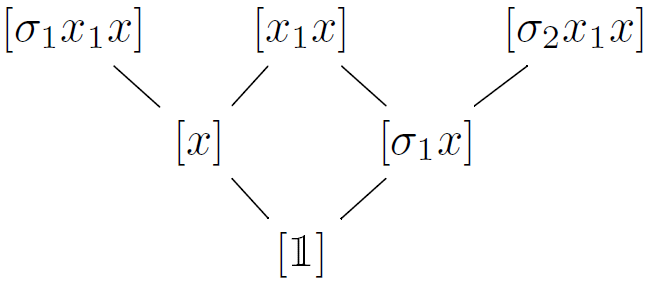Röver's simple group is of type F∞, with Francesco Matucci We prove that the finitely presented simple group constructed by Claas Röver from Thompson's group V and Grigorchuk's group has type F∞. The proof involves constructing a polysimiplicial complex on which Röver's group acts, and then using a combination of Brown's criterion and Bestvina–Brady Morse theory. This result was subsequently generalized by Rachel Skipper and Matthew Zaremsky, and Volodymyr Nekrashevych has conjectured that it holds for all Röver–Nekrashevych groups constructed from contracting self-similar groups. |
 |
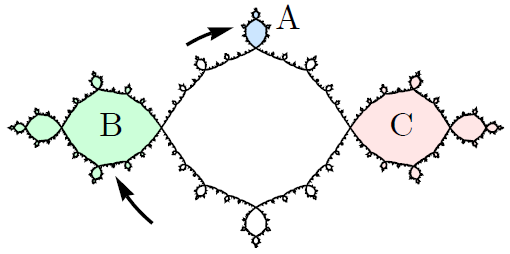A Thompson group for the basilica, with Bradley Forrest We define a Thompson-like group of homeomorphisms of the basilica Julia set, and we prove that this group is finitely generated, virtually simple, and bi‑embeddable with Thompson's group T. Matthew Zaremsky and Stefan Witzel have subsequently proven that the basilica Thompson group is not finitely presented, and Mikhail Lyubich and Sergei Merenkov have shown that this group acts on the basilica by quasisymmetries. |
 |
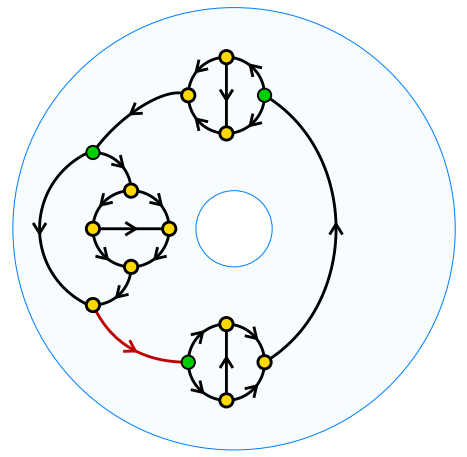
The word problem for finitely presented quandles is undecidable CSPs and connectedness: P/NP dichotomy for idempotent, right quasigroups, with Robert McGrail, Solomon Garber, Japheth Wood, and Benjamin Fish These computer science publications are part of Robert McGrail's research program exploring constraint satisfaction problems in quandles. |
 |
Implementation of a solution to the conjugacy problem in Thompson's group F, with Nabil Hossain, Francesco Matucci, and Robert McGrail Deciding conjugacy in Thompson's group F in linear time These computer science publications describe a Java implementation of the solution to the conjugacy problem in Thompson's group F, and include a proof that the algorithm has linear time complexity. |
 |
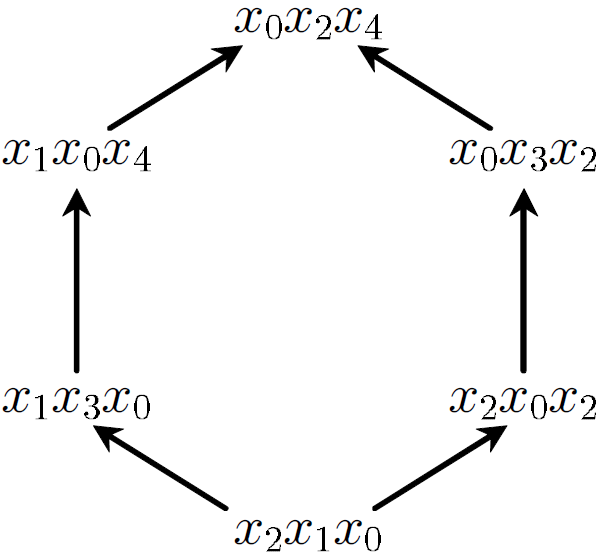
Conjugacy and dynamics in Thompson's groups, with Francesco Matucci We describe strand diagrams for elements of F, T, and V, and we use them to give a unified solution to the conjugacy problems in the three Thompson groups. This includes the first known solution to the conjugacy problem in Thompson's group T. Julio Aroca subsequently generalized our work to a family of Thompson-like groups, and Gil Goffer and Waltraud Lederle used strand diagrams in their analysis of conjugacy for almost automorphisms of trees. |
 |
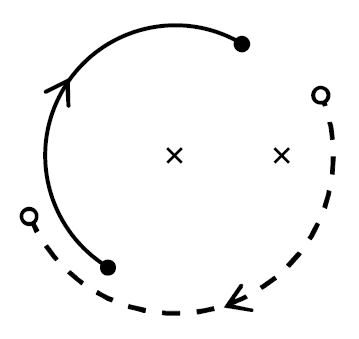Iterated monodromy for a two-dimensional map, with Sarah Koch The paper is a mix of group theory and complex dynamics. We compute the wreath recursion for the iterated monodromy group of a postcritically finite map on CP2, the first explicit computation of its kind. |
 |
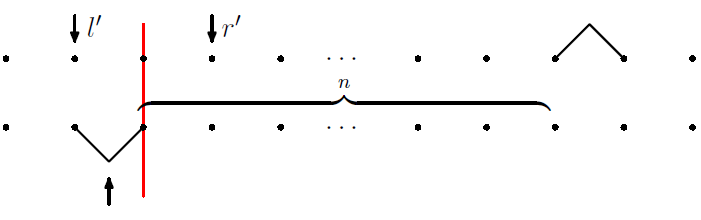Thompson's group F is maximally nonconvex, with Kai‑Uwe Bux This paper was a portion of my PhD thesis. We use forest diagrams to prove that balls in the Cayley graph of F are highly non-convex, a result with was subsequently generalized by Wladis. One consequence is that the Cayley graph of F contains isometrically embedded geodesic circles of arbitrary size. |
 |
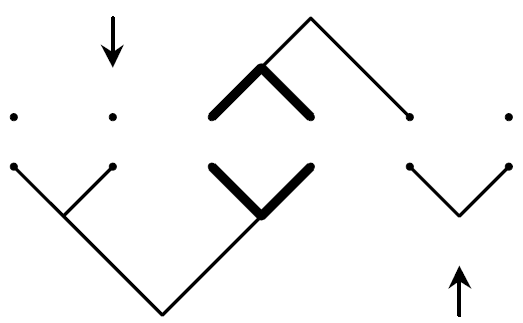Forest diagrams for elements of Thompson's group F, with Kenneth S. Brown This paper was a portion of my PhD thesis. We describe forest diagrams for elements of Thompson's group F, which are particularly well-suited to studying the Cayley graph of F with respect to the {x0, x1} generating set. Using forest diagrams, we give a simplified version of Fordham's length formula for F, and I use them in my PhD thesis to prove that the isoperimetric constant (or Cheeger constant) of F is at most 1/2. |
 |
Thompson's group F This was my PhD thesis under my advisor Kenneth S. Brown. This starts with a fairly complete exposition of the basic theory of Thompson's group F. In addition to material published elsewhere, this also includes a proof that the isoperimetric constant (or Cheeger constant) of F is at most 1/2, a discussion of one-way forest diagrams, a description of word graphs for positive elements and anti-normal form, an introduction to strand diagrams for F and a description of a corresponding classifying space for F (later fleshed out by Sabalka and Zaremsky), and a description of a system for constructing generalized Thompson groups using categories which is related to the cloning systems developed by Witzel and Zaremsky. |